CS61A——环境（含HW-02全）

发表于 分类于 ，
UC Berkeley CS61A —— The Structure and Interpretation of Computer Programs —— Lecture 5 —— 环境

大纲

  1. 多环境；
  2. 高阶函数的环境；
  3. 局部命名；
  4. 函数组合；
  5. 自引用函数；
  6. 柯里化（Currying）；

多环境

函数的生命周期

  1. def语句

    1
    2
    def square(x):
        return x * x
    1. 创建了一个新的函数；
    2. 命名在当前帧绑定到函数上；

  2. 调用表达式

    1
    square(2 + 2)
    1. 求操作符和操作数的值；
    2. 在参数（操作数的值）上调用函数（操作符的值）；

  3. 调用/应用（Calling/applying）

    1. 创建一个新的帧；
    2. 实参（parameter）绑定到形参（argument）上；
    3. 函数体在新的环境中执行；

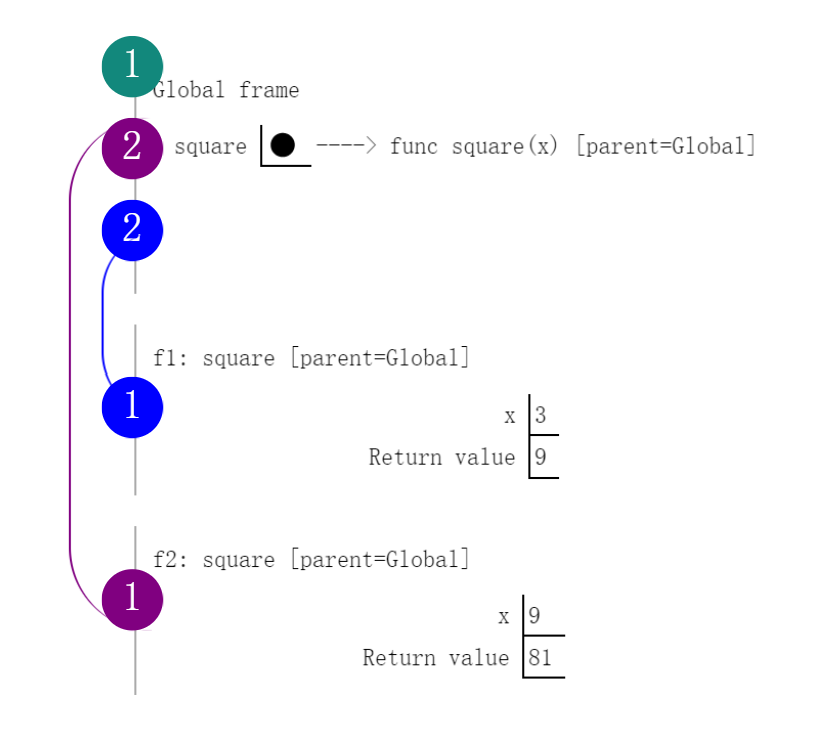
嵌套的调用表达式（多环境）

1
2
3
4
def square(x):
    return x * x

square(square(3))
image-20220106132237027

一个环境由一个帧序列组成：

  1. 环境（绿色）：全局帧；
  2. 环境（蓝色）：局部帧（f1），然后全局帧；
  3. 环境（紫色）：局部帧（f2），然后全局帧；

脱离环境谈命名是没有意义的，每个表达式都在一个环境的上下文中求值。

命名求值为 找到该命名的 当前环境的 最早帧中绑定到该名称 的 值。

不同环境中命名有不同的意义

1
2
3
4
def square(square):
    return square * square

square(4)

在全局环境中，square绑定为函数，在局部环境中，square绑定为局部变量。

高阶函数的环境

回顾

高阶函数是：

  1. 以函数为形参的函数；
  2. 或返回值为函数的函数；

函数是第一等级（first class）：函数在Python中是值（value）。

note

在函数式语言中，可以对函数像值或对象实例一样进行绑定在变量上或者作为参数来传递的操作。

第一等级满足的特征：

  1. 可以存放在变量和数据结构中；
  2. 可以当做参数传递给子过程；
  3. 可以当做子过程的返回值；
  4. 可以在运行期间被创建。

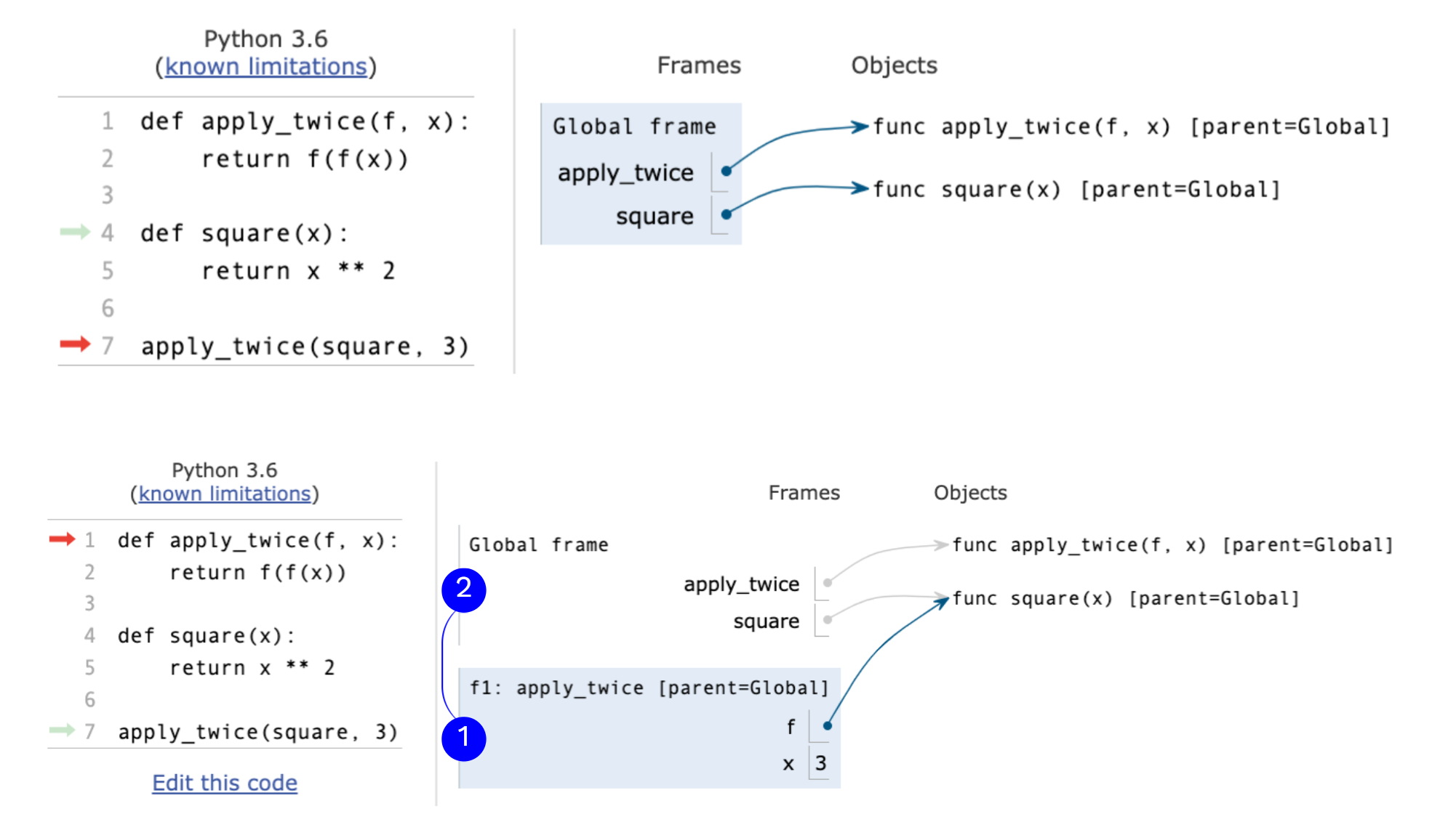
一个应用两次函数的例子

1
2
3
4
5
6
7
def apply_twice(f, x):
    return f(f(x))

def square(x):
    return x ** 2

apply_twice(square, 3)

参数绑定到了函数上：

image-20220106134011321

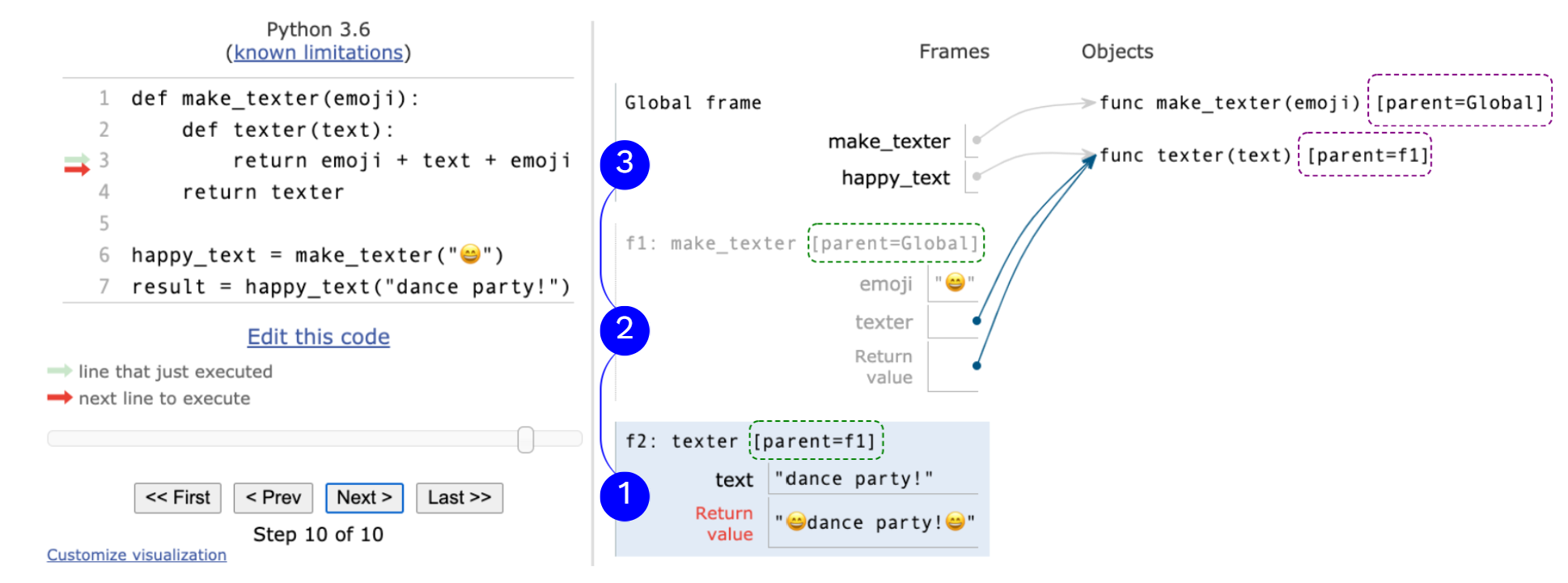
嵌套定义的环境

一个嵌套定义函数并返回函数的例子

1
2
3
4
5
6
7
def make_texter(emoji):
    def texter(text):
        return emoji + text + emoji
    return texter

happy_text = make_texter("😄")
result = happy_text("lets go to the beach!")

image-20220106134352867

  1. 每个用户定义的函数都有个父帧；
  2. 函数的父帧是其定义所在的帧；
  3. 每个局部帧都有个父帧；
  4. 帧的父帧是其相应的被调用函数的父帧；
  5. 环境是帧的序列。

如何绘制环境图

定义函数时

  1. 创建一个函数变量：

    1
    func <name>(<formal parameters>) [parent=<label>]

  2. 它的父帧为当前帧；

  3. 绑定<name>到当前帧的函数值；

调用函数时

  1. 添加一个局部帧，标题为被调用的函数的<name>；
  2. 复制函数的父帧到局部帧：[parent=<label>]；
  3. 绑定<formal parameters>到局部帧的实参；
  4. 在以局部帧为开始的环境中执行函数体。

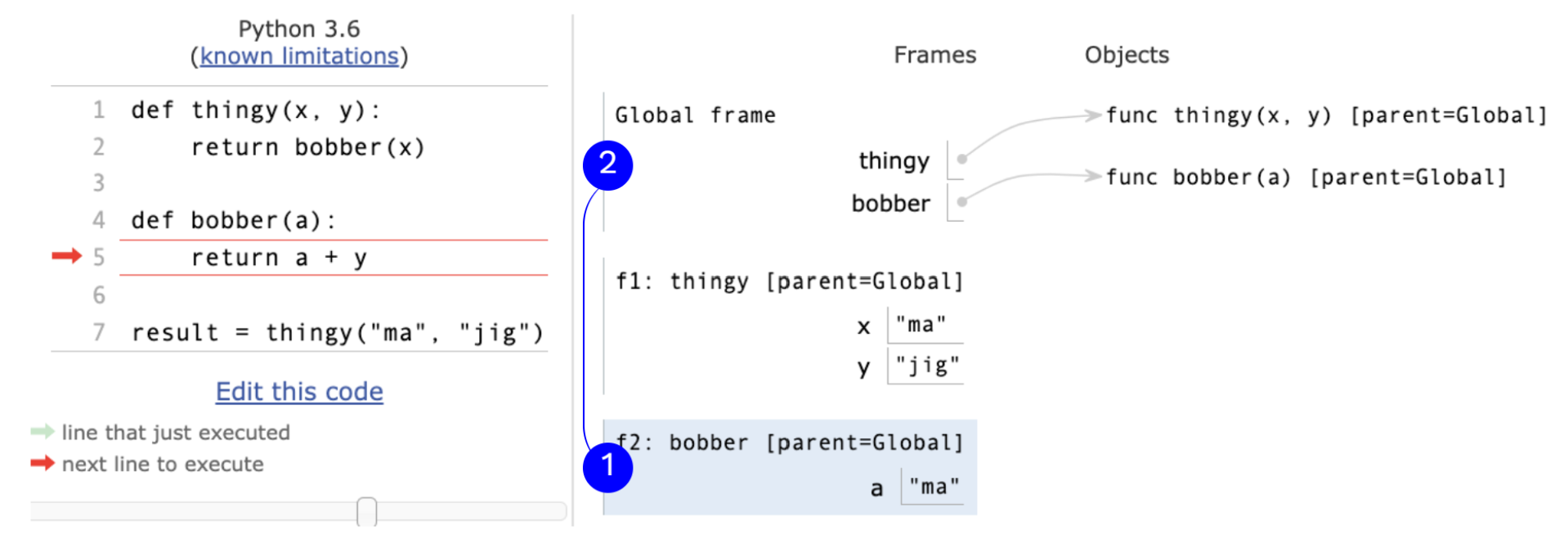
局部命名

一个例子

1
2
3
4
5
6
7
def thingy(x, y):
    return bobber(y)

def bobber(a):
    return a + y

result = thingy("ma", "jig")

这个例子会报错，bobber中y未定义的NameError

局部命名可见性

局部命名对于其他非嵌套的函数不可见。

调用一个顶级函数会创建一个环境，这个环境包括一个局部帧后面跟着全局帧。

image-20220106135729306

函数组合

一个函数组合器的例子

1
2
3
4
5
6
7
8
9
10
11
12
13
def happy(text):
    return "☻" + text + "☻"

def sad(text):
    return "☹" + text + "☹"

def composer(f, g):
    def composed(x):
        return f(g(x))
    return composed

msg1 = composer(sad, happy)("cs61a!")
msg2 = composer(happy, sad)("eecs16a!")

另一个函数组合器的例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def happy(text):
    return "☻" + text + "☻"

def sad(text):
    return "☹" + text + "☹"

def make_texter(emoji):
    def texter(text):
        return emoji + text + emoji
    return texter

def composer(f, g):
    def composed(x):
        return f(g(x))
    return composed

composer(happy, make_texter("☃︎"))('snow day!')

被组合的函数之一可能是个高阶函数。

image-20220106140502775

自引用

一个自引用的函数

高阶函数可以返回一个引用它自身命名的函数：

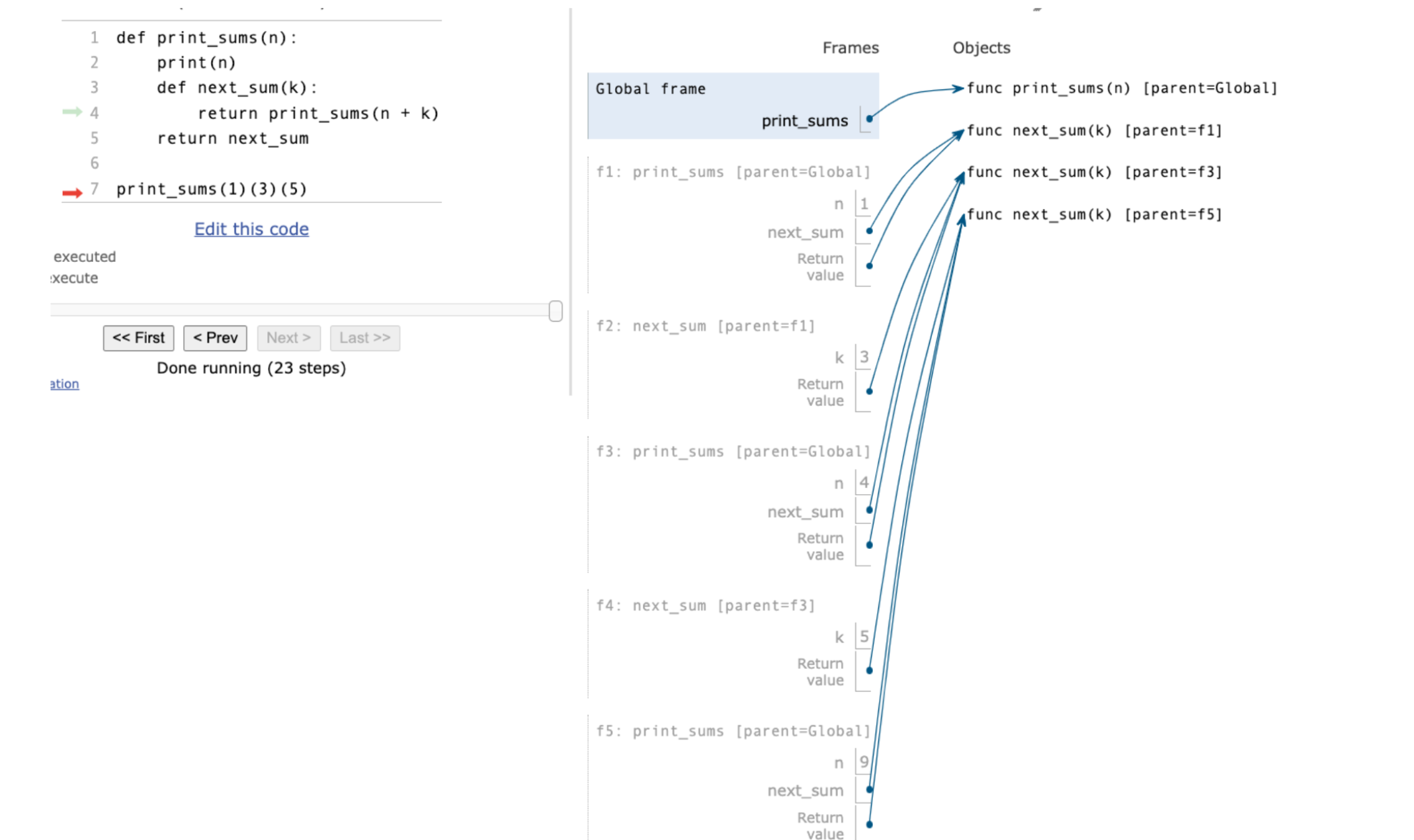
1
2
3
4
5
6
7
def print_sums(n):
    print(n)
    def next_sum(k):
        return print_sums(n + k)
    return next_sum

print_sums(1)(3)(5)

输出为：

1
2
3
4
1
4
9
<function print_sums.<locals>.next_sum at 0x0000019AA5581CA0>

image-20220106140938332

理解print_sums

调用为：

1
print_sums(1)(3)(5)

等价于：

1
2
3
g1 = print_sums(1)
g2 = g1(3)
g2(5)

调用print_sums(x)会返回一个函数：

  1. 副作用是打印x；
  2. 返回一个函数，这个函数输入是参数x+y，但这个函数做的事和print_sums()一样；

所以过程为：

  1. 打印1，返回g1；
  2. 调用g1打印4，返回g2；
  3. 调用g2打印9，返回另一个函数；

柯里化

add vs. make_adder

比较：

1
2
3
from operator import add

add(2, 3)

和：

1
2
3
4
def make_adder(n):
    return lambda x: n + x

make_adder(2)(3)

前者后者是什么关系呢？

前者直接调用了一个函数，输入是两个操作数；

后者调用的函数返回了一个加法函数，输入是另一个数。

函数柯里化（Currying）

柯里化：把一个多参数的函数转换为单参数的高阶函数。

一个将任意二参数函数柯里化的函数：

1
2
3
4
5
6
def curry2(f):
    def g(x):
        def h(y):
            return f(x, y)
        return h
    return g

调用：

1
2
make_adder = curry2(add)
make_adder(2)(3)

另一个定义方式：

1
curry2 = lambda f: lambda x: lambda y: f(x, y)

为什么柯里化？

以美国逻辑学家 Haskell Curry 的名字命名，但实际上首先由俄罗斯人Moses Schönfinkel基于德国人Gottlob Frege提出的原则发表。（在1980发表的一篇文章中，他提出了Stigler定律——科学规律往往都不是以原创者的名字命名的，而是以后来更有名望的学者的名字加以命名。Stigler’s law of eponymy - Wikipedia）

有些分析手段只能处理单参数的函数，柯里化之后就可以应用这些手段了。

Homework

Product

课上学的summation(n, term)函数实现了term(x)的累加，现在要求写个类似的累乘：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def product(n, term):
    """Return the product of the first n terms in a sequence.

    n: a positive integer
    term:  a function that takes one argument to produce the term

    >>> product(3, identity)  # 1 * 2 * 3
    6
    >>> product(5, identity)  # 1 * 2 * 3 * 4 * 5
    120
    >>> product(3, square)    # 1^2 * 2^2 * 3^2
    36
    >>> product(5, square)    # 1^2 * 2^2 * 3^2 * 4^2 * 5^2
    14400
    >>> product(3, increment) # (1+1) * (2+1) * (3+1)
    24
    >>> product(3, triple)    # 1*3 * 2*3 * 3*3
    162
    """
    "*** YOUR CODE HERE ***"

很简单，一个循环就行了：

1
2
3
4
5
6
7
def product(n, term):
    result = 1
    k = 1
    while k <= n:
        result = result * term(k)
        k = k + 1
    return result

Accumulate

现在向把summation和product一般化，把累加和累成一般化为accumulate：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def accumulate(merger, base, n, term):
    """Return the result of merging the first n terms in a sequence and base.
    The terms to be merged are term(1), term(2), ..., term(n). merger is a
    two-argument commutative function.

    >>> accumulate(add, 0, 5, identity)  # 0 + 1 + 2 + 3 + 4 + 5
    15
    >>> accumulate(add, 11, 5, identity) # 11 + 1 + 2 + 3 + 4 + 5
    26
    >>> accumulate(add, 11, 0, identity) # 11
    11
    >>> accumulate(add, 11, 3, square)   # 11 + 1^2 + 2^2 + 3^2
    25
    >>> accumulate(mul, 2, 3, square)    # 2 * 1^2 * 2^2 * 3^2
    72
    >>> # 2 + (1^2 + 1) + (2^2 + 1) + (3^2 + 1)
    >>> accumulate(lambda x, y: x + y + 1, 2, 3, square)
    19
    >>> # ((2 * 1^2 * 2) * 2^2 * 2) * 3^2 * 2
    >>> accumulate(lambda x, y: 2 * x * y, 2, 3, square)
    576
    >>> accumulate(lambda x, y: (x + y) % 17, 19, 20, square)
    16
    """
    "*** YOUR CODE HERE ***"
    
def summation_using_accumulate(n, term):
    """Returns the sum: term(1) + ... + term(n), using accumulate.

    >>> summation_using_accumulate(5, square)
    55
    >>> summation_using_accumulate(5, triple)
    45
    """
    "*** YOUR CODE HERE ***"

def product_using_accumulate(n, term):
    """Returns the product: term(1) * ... * term(n), using accumulate.

    >>> product_using_accumulate(4, square)
    576
    >>> product_using_accumulate(6, triple)
    524880
    """
    "*** YOUR CODE HERE ***"

还是很容易啊，就把参数作为运算和基数就行：

1
2
3
4
5
6
7
8
9
10
11
12
13
def accumulate(merger, base, n, term):
    result = base
    k = 1
    while k <= n:
        result = merger(result, term(k))
        k = k + 1
    return result

def summation_using_accumulate(n, term):
    return accumulate(add, 0, n, term)

def product_using_accumulate(n, term):
    return accumulate(mul, 1, n, term)

Church numerals（附加题，Just for fun）

一个叫Alonzo Church的逻辑学家发明了一种完全使用函数表示非负整数的系统，目的是为了说明函数足以描述所有的数论：如果我们有函数，我们就不需要假设数字存在，而可以发明数字。

题目让重新发现这个Church numerals的表示法。

0的定义和一个返回比其参数多一的函数定义如下：

1
2
3
4
5
def zero(f):
    return lambda x: x

def successor(n):
    return lambda f: lambda x: f(n(f)(x))

要求：

  1. 定义1和2，他们的行为分别和successor(zero)、successor(successor(zero))是一样的但别直接调用successor；
  2. 实现一个函数church_to_int把一个Church数变成一个常规的Python整数；
  3. 实现函数add_church、mul_church和pow_church，分别执行church数上得加法、乘法和指数运算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
def one(f):
    """Church numeral 1: same as successor(zero)"""
    "*** YOUR CODE HERE ***"

def two(f):
    """Church numeral 2: same as successor(successor(zero))"""
    "*** YOUR CODE HERE ***"

three = successor(two)

def church_to_int(n):
    """Convert the Church numeral n to a Python integer.

    >>> church_to_int(zero)
    0
    >>> church_to_int(one)
    1
    >>> church_to_int(two)
    2
    >>> church_to_int(three)
    3
    """
    "*** YOUR CODE HERE ***"

def add_church(m, n):
    """Return the Church numeral for m + n, for Church numerals m and n.

    >>> church_to_int(add_church(two, three))
    5
    """
    "*** YOUR CODE HERE ***"

def mul_church(m, n):
    """Return the Church numeral for m * n, for Church numerals m and n.

    >>> four = successor(three)
    >>> church_to_int(mul_church(two, three))
    6
    >>> church_to_int(mul_church(three, four))
    12
    """
    "*** YOUR CODE HERE ***"

def pow_church(m, n):
    """Return the Church numeral m ** n, for Church numerals m and n.

    >>> church_to_int(pow_church(two, three))
    8
    >>> church_to_int(pow_church(three, two))
    9
    """
    "*** YOUR CODE HERE ***"

首先分析这个函数：

1
2
def zero(f):
    return lambda x: x

就返回一个函数，这个函数输入是自己，返回值也是自己。

然后再分析这个函数：

1
2
def successor(n):
    return lambda f: lambda x: f(n(f)(x))

输入是n，返回一个lambda函数，这个lambda函数输入是f，返回值也是一个lambda表达式，这个表达式输入是x，返回值是f(n(f)(x))。

那我们写出successor(zero)，返回值是：

1
lambda f: lambda x: f(zero(f)(x))

zero(f)(x)就等价于x，所以上面的等价于：

1
lambda f: lambda x: f(x)

这是个lambda函数，参数值为f，返回值为lambda x: f(x)，因此one(f)定义如下：

1
2
def one(f):
    return lambda x: f(x)

同理，successor(one)就是：

1
lambda f: lambda x: f(one(f)(x))

即：

1
lambda f: lambda x: f((x))

所以同理，two(f)定义为：

1
2
def two(f):
    return lambda x: f(f(x))

那其实已经很明显了，数字几就等价于church数的几层嵌套函数。

那把church数变成整数的思路就有了，每次嵌套调用的时候加一就行，对于church数n，给他的参数就是f，我们给一个匿名加一的函数lambda x: x + 1，嵌套到最里层，函数的输入是0：

1
2
def church_to_int(n):
    return n(lambda x: x + 1)(0)

用嵌套的思路来理解，那么加法就是进一步嵌套：

1
2
def add_church(m, n):
    return lambda f: lambda x: m(f)(n(f)(x))

乘法就是俄罗斯套娃，把n(f)作为新的f：

1
2
def mul_church(m, n):
    return lambda f: m(n(f))

指数运算我也没想出来有什么优美的方式，直到看到了别人给的答案：

1
2
def pow_church(m, n):
    return n(m)

n(f)可以理解为嵌套了n次f，也就是f(f(...f(...)))。

那么n(f)(x)就是f(f(...f(...)))，所以m(f)(n(f)(x))就是f(f(...f(n(f)(x))))，也就是嵌套了m + n层。

那么m(n(f))就是n(f)(n(f)...n(f)(...))，展开就是m * n层。

所以！n(m)就是m(m(m...m(f)))展开就是m * m * ... * m层，即m的n次方，妙啊！