CS61A——高阶函数

发表于 分类于 ，
UC Berkeley CS61A —— The Structure and Interpretation of Computer Programs —— Lecture 4 —— 高阶函数

纲要

  1. 迭代例子
  2. 设计函数
  3. 一般化
  4. 高阶函数
  5. lambda表达式
  6. 条件表达式

迭代例子

维拉汉卡-斐波那契数字

1
0  1  1  2  3  5  8  13  21  34

从第三个数开始，每个数都等于前两项的和。

维拉汉卡问题

对于一个总时长有多少种节奏存在？

S表示短音节，L表示长音节，一个长音节等于两个短音节。

时长 Meters 总可能性
1 S 1
2 SS，L 2
3 SSS，SL，LS 3
4 SSSS，SSL，SLS，LSS，LL 5
5 SSSSS，SSSL，SSLS，SLSS，SLL，LLS，LSL，LSSS 8

斐波那契问题

一对兔子每个月可以生一对兔子，N个月后有多少对兔子？

维拉汉卡-斐波那契数字生成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def vf_number(n):
    """Compute the nth Virahanka-Fibonacci number, for N >= 1.
    >>> vf_number(2)
    1
    >>> vf_number(6)
    8
    """ 
    prev = 0  # First Fibonacci number
    curr = 1  # Second Fibonacci number
    k = 1
    while k < n: 
        (prev, curr) = (curr, prev + curr)
        k += 1
    return curr

这里用了个循环来解决。

黄金螺旋

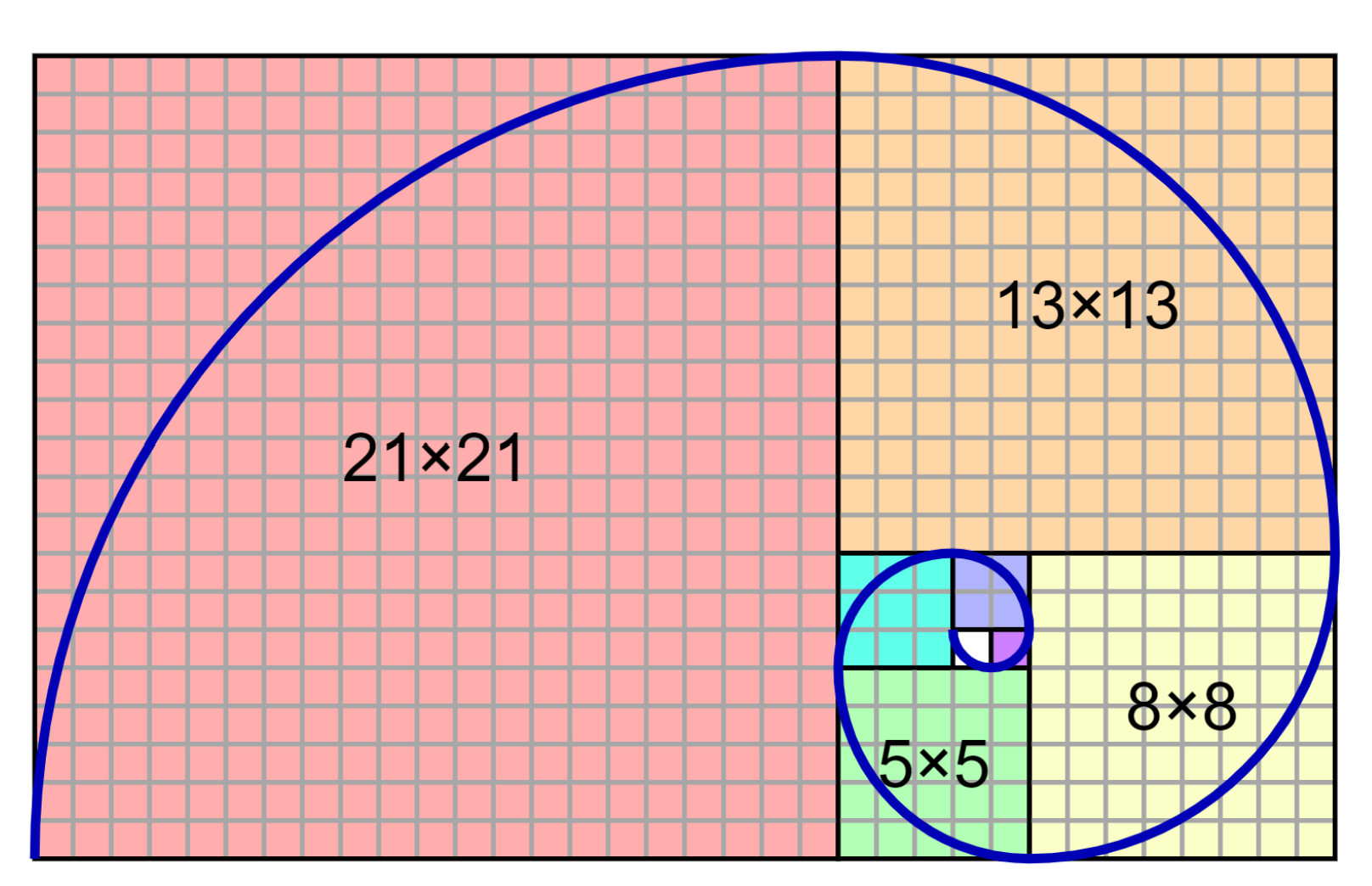
image-20220105005019911

黄金螺旋也可以近似看做维拉汉卡-斐波那契数列。

据说熊身上都有黄金螺旋，多少有点强行了。

image-20220105005210508

设计函数

描述函数

1
2
3
def square(x):
    """Returns the square of x."""
    return x * x
Aspects Examples
一个函数的域（domain）是通过参数得到的所有输入的集合 x是一个数
一个函数的范围（range）是其返回的输出的值的集合 square返回一个非负实数
一个纯函数的行为（behavior） square返回x的平方

定义一个函数

只给一个函数一个工作，但让其适应很多相关情形：

1
2
3
4
round(1.23)     # 1
round(1.23, 0)  # 1
round(1.23, 1)  # 1.2
round(1.23, 5)  # 1.23

别自己重复（DRY，Don’t Repeat Yourself）：只实现一个过程，执行很多次。

一般化

通过参数一般化模式

几何形状有相似的面积公式：

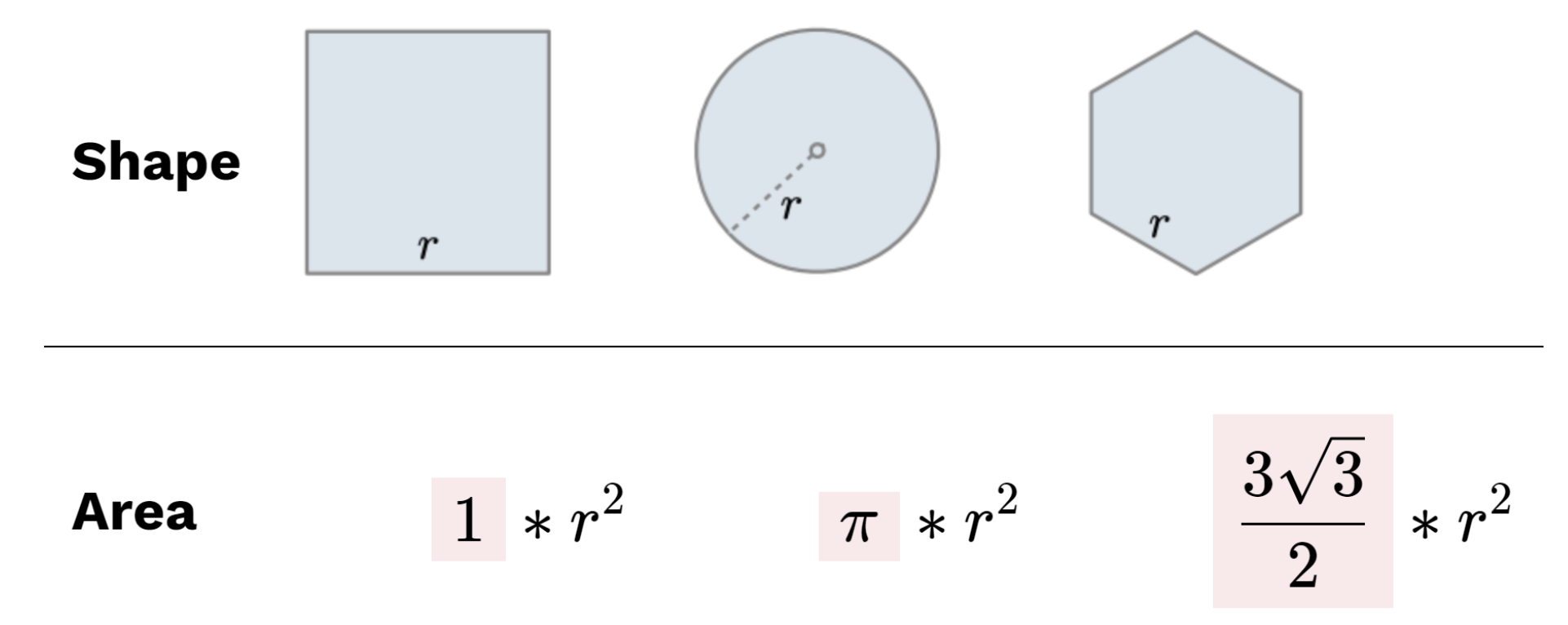
image-20220105010215638

一个非一般化的方法

1
2
3
4
5
6
7
8
9
10
from math import pi, sqrt

def area_square(r):
    return r * r

def area_circle(r):
    return r * r * pi

def area_hexagon(r):
    return r * r * (3 * sqrt(3) / 2)

怎么一般化共同结构呢？

一般化的面积函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from math import pi, sqrt

def area(r, shape_constant):
    """Return the area of a shape from length measurement R."""
    if r < 0:
        return 0
    return r * r * shape_constant

def area_square(r):
    return area(r, 1)

def area_circle(r):
    return area(r, pi)

def area_hexagon(r):
    return area(r, 3 * sqrt(3) / 2)

高阶函数

什么是高阶函数

满足两者之一的函数都是高阶方程：

  1. 以其他函数为参数；
  2. 返回一个函数作为它的结果；

其他函数都认为是一阶方程。

计算过程上的一般化

函数间的共同结构可能是一个计算过程，而不止是一个数，比如：

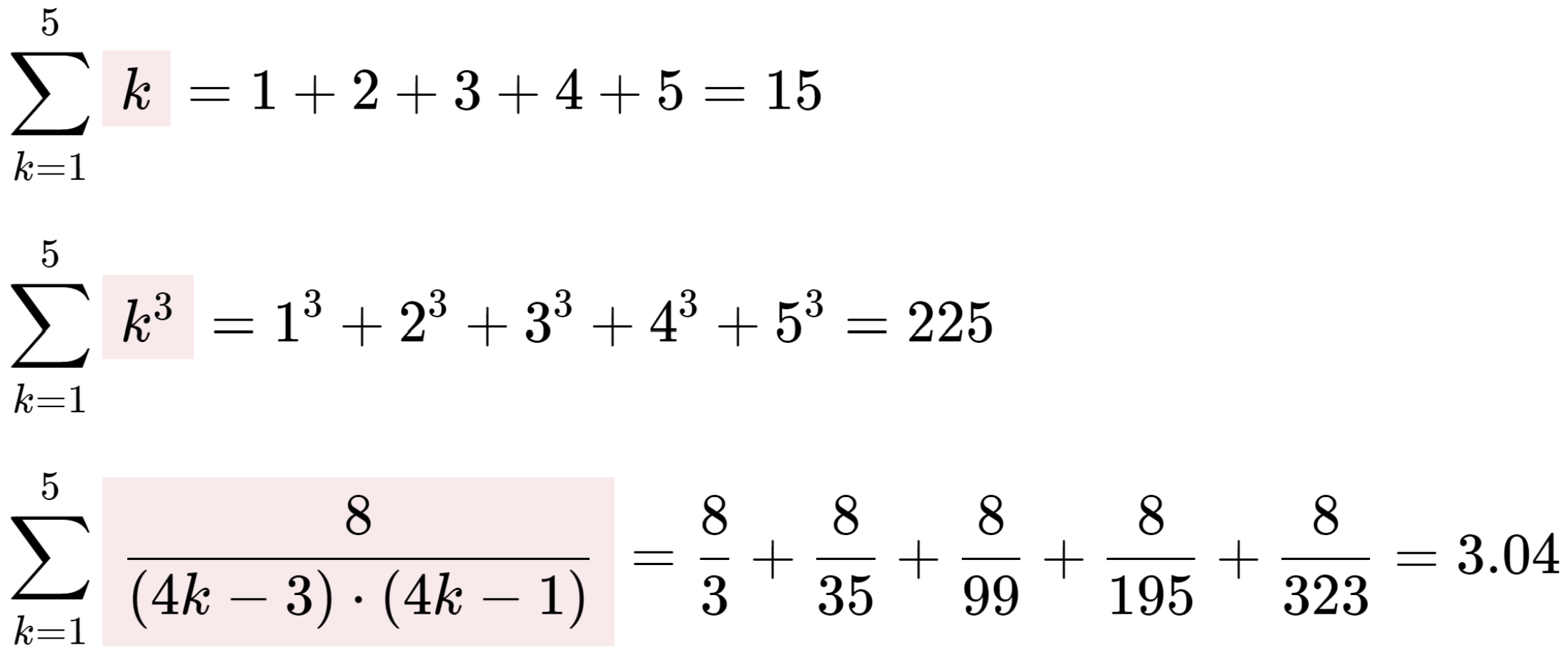
image-20220105010805023

函数作为参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def cube(k):
    return k ** 3

def summation(n, term):
    """Sum the first N terms of a sequence.
    >>> summation(5, cube)
    225
    """
    total = 0
    k = 1
    while k <= n:
        total = total + term(k)
        k = k + 1
    return total

函数作为返回值

局部定义的函数

定义在其他函数体内的函数会绑定到局部帧的命名。

1
2
3
4
5
6
7
8
9
10
def make_adder(n):
    """Return a function that takes one argument k
       and returns k + n.
    >>> add_three = make_adder(3)
    >>> add_three(4)
    7
    """
    def adder(k):
        return k + n
    return adder

调用表达式作为操作符表达式

1
make_adder(1)(2)

make_adder(1)调用了函数，返回了一个函数又作为函数被调用。

Lambda表达式

lambda语法

lambda表达式是一种简单的函数定义，计算结果是一个函数，语法为：

1
lambda <parameters>: <expression>

返回的函数以parameters为输入并返回expression计算的值。

比如，lambda版本的square函数：

1
square = lambda x: x * x

会返回一个函数，以x为参数，返回x * x作为结果。

Lambda语法提示

lambda表达里面不应该包含return语句，如：

错误用法：

1
square = lambda x: return x * x

def语句和lambda表达式对比

1
2
3
4
5
6
# def语句
def square(x):
    return x * x

# lambda语句
square = lambda x: x * x

共同点：

  1. 都创建了一个函数，域、范围和行为都一样；
  2. 都把函数绑定到了square上；

不同点：

只有def语句给了函数一个固有名称，可以在环境图中看到，但不影响执行，只在打印的时候有区别。

image-20220105012645366

lambda作为参数

要把简单函数作为参数的时候用lambda表达式很方便：

1
2
3
4
5
6
7
8
# 原始方法
def cube(k):
    return k ** 3

summation(5, cube)

# 用lambda表达式
summation(5, lambda k: k ** 3)

条件表达式

条件表达式

条件表达式格式如下：

1
<consequent> if <predicate> else <alternative>

规则是这样的：

  1. 求<predicate>的值；
  2. 如果值为真，整个表达式的值为<consequent>;
  3. 否则，表达式的值为<alternative>。

有条件表达式的lambda语句

错误语法：

1
lambda x: if x > 0: x else: 0	# 不能有冒号

正确语法：

1
lambda x: x if x > 0 else 0